A-Level数学解析：向量知多少?

　　线性代数在很多领域都有应用

　　·  物理

　　· 电力工程

　　· 机械工程

　　· 统计

　　……

　　学过线性代数的学生可能都会做以下计算，但他们却不知道为什么要这样计算，它们分别代表的含义是什么?学生们对于线性代数中的几何意义的理解是非常模糊的

　　·  matrix multiplication - 矩阵乘法

　　·  the Determinant - 行列式

　　·  cross products - 交叉乘积

　　·  eigenvalues - 特征值

　　实际上，理解线性代数的几何意义，有助于在你遇到具体问题的时候，知道用什么工具去解决它们，这些工具为什么有效，并且对产生的结果做出解释。而理解线性代数的算术意义，只能够帮你在使用这些工具的时候，完成整个计算过程。所以学习线性代数的层次关系应该是，由底向上：几何意义 -> 算术意义 -> 应用

　　于是，面对线性代数问题，人们更应该把计算部分交给计算机来完成，自己则专注于概念和原理部分。

　　向量是线性代数基本构成要素的根源。不同的职业对向量有不同的视角：

　　物理系学生对向量的视角：vectors are arrows pointing in space.

　　What defines a given vector is its length, and the direction it's pointing in.

　　计算机专业同学的视角：vectors are ordered lists of numbers. 2-dimensional is the fact that the length of that list is 2.

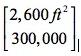
　　数学专业的同学：generalize both of these views (线性代数中所有的课题都是围绕这两种操作进行的)：

　　1. 两个向量相加

　　2. 用一个常数和另一个向量相乘

　　Vector - 在坐标系中的有箭头的线段，它的末尾总在原点上，在2维空间中，向量(i、j)的第 1 个数字 i是尖端落在 x轴的长度，第 2 个数字j是尖端落在 y轴的长度，如果落在原点的左边(x 轴)和下边(y 轴)，则 i、j 的值为负数;在 3 维空间中，每个向量有 3 个数(i、j、k)来表示，分别是尖端落在 x、y、z 轴上的长度，x、y、z 同样是有符号的。